Lessons From Parallelizing Matrix Multiplication

Before you dismiss this as yet another boring matrix multiplication example, consider that this, this, this and a lot of other tutorials on the web all use a naive version of matrix multiplication and then attempt to parallelize that version of it to demonstrate how to speed things up using some technology.

What do I mean by a naive version (since there are many naive ways of doing things depending on the system that we are talking about)? This is the basic C++ code for matrix multiplication used in most examples:

void matmult(int m, int n, int p, double **A, double **B, double **C) {
  for (int i = 0; i < m; i++) {
    for (int j = 0; j < n; j++) {
      for (int k = 0; k < p; k++) {
        C[i][j] += A[i][k] * B[k][j];
      }
    }
  }
}

And this is the smarter version which shouldn't surprise anyone who has taken a computer architecture course:

void matmult(int m, int n, int p, double **A, double **B, double **C) {
  for (int i = 0; i < m; i++) {
    for (int k = 0; k < p; k++) {
      for (int j = 0; j < n; j++) {
        C[i][j] += A[i][k] * B[k][j];
      }
    }
  }
}

What's the difference? The difference is pretty subtle so you might have missed it: the inner loops have been swapped i.e. the j and k iterations.

What can changing two lines do? After all, the results are the same right? Well, take a look at this output from the Shark profiler tool in OS X.

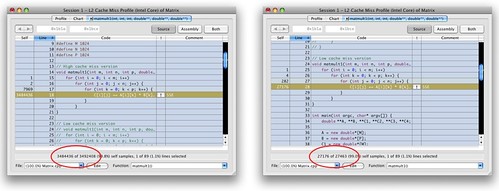
The version on the left uses the naive algorithm and has 3 484 436 L2 cache misses for a 1024 x 1024 matrix multiplication. The version on the right uses the smarter algorithm and has 27 176 L2 cache misses. On my Core Duo MacBook Pro, the naive version runs in 52 133 ms and the smarter algorithm runs in 13 730 ms. That's nearly a 4x speedup and we didn't even parallelize anything yet!

Hopefully that last line caught your attention. That's the result on my MacBook Pro with a fairly old two-core processor. Let's run some experiments on a 24-core machine (6 cores per socket) using Intel Xeon CPU E7450 @ 2.40GHz running Linux 2.6.18. The code was compiled using g++-4.2 with -O3.

The naive version runs in 15 962 ms. The smarter version runs in 1 860 ms. Let's try parallelizing the naive version with OpenMP:

void matmult(int m, int n, int p, double **A, double **B, double **C) {
#pragma openmp parallel for
  for (int i = 0; i < m; i++) {
    for (int j = 0; j < n; j++) {
      for (int k = 0; k < p; k++) {
        C[i][j] += A[i][k] * B[k][j];
      }
    }
  }
}

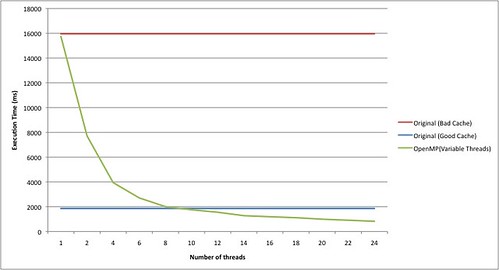
Notice that we need to use ~9 threads to break even with the smarter version. Incidentally, if we use the smarter algorithm and parallelize it using 24 threads, it runs in 151 ms!

So what are the lessons from this?

• Low level details matter for performance - I think it's important to mention those details when parallelizing. We needed quite a few threads (9 threads) before you can break even with the smarter algorithm. And most machines today don't have that many cores yet. And as long as the future manycore machines continue to use hierarchical memory (L1, L2, L3 caches), such memory optimization techniques will always be useful. In fact such optimizations help improve performance even if you are running Java or .NET on a virtual machine. However, ...
• Low level optimizations can get tricky - this example is simple since we are only swapping the iterations to reduce cache misses. But some other optimizations e.g. tiling require more invasive transformations which is why ...
• Always advice your users to use well-tuned libraries whenever possible. Matrix multiplication is a well-known algorithm and there are plenty of better ways to do it (look at BLAS and ATLAS). It's a disservice to give users the impression that they should write their own matrix multiplication routine when well-tuned ones are easily available. And that's why, we need to ...
• Pick better and more interesting examples to parallelize. Matrix multiplication is embarrassingly parallel; the hard part is trying to wrestle with the memory hierarchy to ensure performance. For some other problems, it's hard to see what each thread should do and how to coordinate those threads. So instead, people should put in effort into documenting those more complicated parallelizing techniques into patterns for parallel programming. That's the real test of how good your parallel library/framework/language is.